Table of Contents

  1. Introduction
  2. Applications
  3. Number Theory
  4. DHKE steps
  5. Need for primitive root
  6. Discrete Logarithm Problem (DLP)
  7. Solving DLP
  8. Attacks on DHKE
  9. DH in real life
  10. Additional resources

Introduction

The Diffie-Hellman key exchange (DHKE), proposed by Whitfield Diffie and Martin Hellman in 1976, was the first asymmetric scheme published in the open literature. They were also influenced by the work of Ralph Merkle. DHKE provides a practical solution to the key distribution problem, i.e., it enables two parties to derive a common secret key by communicating over an insecure channel. DHKE is a very impressive application of the discrete logarithm problem. There was a patent US patent 4200770 for this protocol but it expired in 1997.

[Q] Wait what?! The patent mentions “Merkle; Ralph C. (Palo Alto, CA)” as an inventor. Why don’t we call this diffie-hellman-merkle protocol?

[A] Well, Martin Hellman acknowledges it too. His paper “AN OVERVIEW OF PUBLIC KEY CRYPTOGRAPHY” mentions: “… system in this paper has since become known as Diffie-Hellman key exchange. While that system was first described in a paper by Diffie and me, it is a public key distribution system, a concept developed by Merkle, and hence should be called “Diffie-Hellman-Merkle key exchange” if names are to be associated with it. I hope this small pulpit might help in that endeavor to recognize Merkle’s equal contribution to the invention of public key cryptography. Space does not permit an explanation of the quirk of fate that seems to have deprived Merkle of the credit he deserves, but a quirk it is”

Since Martin himself thinks this is a quirk of fate, I don’t think I have a better explanation.

However, there’s an interesting story behind Ralph C. Merkle about … Apologies for digressing. I’ll tell the story at the end of article.

Applications

The fundamental key agreement technique is implemented in many open and commercial cryptographic protocols like Secure Shell (SSH), Transport Layer Security (TLS), and Internet Protocol Security (IPSec). If you’ve ever transferred/received money online (domestic/international), if you’ve ever paid your phone/internet/water/apartment/utilities bill online, if you’ve ever paid your tuition fee online, if you’ve booked a hotel room online, if you’ve purchased air/train/bus tickets online, if you’ve purchased anything online on amazon/walmart/wayfair/ebay/alibaba/flipkart/jd (and so on), it is extremely likely that you’ve made use of this key exchange protocol.

Let’s take a moment to thank

Number theory

Order of an element, cyclic group, generator, Euler’s theorem, Euler’s Totient function,…If you are not familiar with any of these terms, I highly recommend brushing up on some elementary number theory. Number Theory Primer is a reference that I use to refresh my memory. You are welcome to read up other materials too.

A lot of mathematicians have spent great amount of time and energy to discover the beauty of numbers and their relationships. It takes a lot of persistence and intelligence to discover these relations. We are just reaping the practical benefits of those theoretical studies. We owe it to those mathematicians to appreciate their work and build on it.

Alice and Bob exchange a large prime p and a primitive root (modulo p) g. Alice picks a private number a and sends ga mod p to Bob and Bob picks a private number b and sends gb mod p to Alice. Alice and Bob now generate gab mod p as their secret key.

There we go, that’s DHKE summarized in 3 sentences.

The whole purpose of knowing DHKE is not just to find out the steps but to understand why it guarantees a secure key exchange. What computationally infeasible problem does it use to create a secure key exchange architecture. What other mathematical problems can be used to build security for the modern world.

DHKE steps

Alice and Bob need to exchange a secret key securely over an insecure channel. Secret key should never be on the insecure channel.

At first glance it appears that Alice and Bob face an impossible task. It was a brilliant insight of Diffie and Hellman that the difficulty of the discrete logarithm problem provides a possible solution.

  1. Alice and Bob to agree on a large prime p and a nonzero integer g (where p is large (typically at least 512 bits) and g is a primitive root modulo p)
  2. Alice and Bob make the values of p and g public knowledge
  3. Alice chooses a large random number a as her private key and Bob similarly chooses a large number b
  4. Alice then computes A = ga mod p, which she sends to Bob and Bob computes B = gb mod p, which he sends to Alice

  5. Both Alice and Bob compute their shared key K=gab mod p, which Alice computes as

    K = Ba mod p = (gb mod p)a mod p

    and Bob computes as

    K = Ab mod p = (ga mod p)b mod p

  6. Alice and Bob can now use their shared key K to exchange information without worrying about other users obtaining this information.

In order for a potential eavesdropper (Eve) to do so, she would first need to obtain K knowing g, p, A and B only. This can be done by computing a from A = ga mod p or b from B = gb mod p This is the discrete logarithm problem, which is computationally infeasible for large p. Computing the discrete logarithm of a number modulo p takes roughly the same amount of time as factoring the product of two primes the same size as p, which is what the security of the RSA cryptosystem relies on.

Why should g be primitive root modulo p?

That’s a great question! The idea of computationally infeasible problem rests on this requirement being satisfied. Before we move on to the why, let’s first understand what is primitive root modulo n.

Programmatic definition: Primitive root of a prime number n is an integer r between [1, n-1] such that the values of rx mod n where x is in range [0, n-2] are different.

Mathematical definition: Let n be a positive integer. A primitive root mod n is an integer g such that every integer relatively prime to n (coprime1 of n) is congruent to a power of g mod n. Integer g is a primitive root (mod n) if for every number a relatively prime to n there is an integer k such that a ≡ gk mod n

Example:

2 is a primitive root mod 5, because for every number a coprime to 5, there is an integer k such that a ≡ 2k (mod 5). For every integer relatively prime to there is a power of that is congruent.

Primitive root modulo n exists if and only if:

  • n is 1, 2, 4, or
  • n is power of an odd prime number (n=pk), or
  • n is twice power of an odd prime number (n=2.pk).

This theorem was proved by Gauss.

Properties:

  • No simple general formula to compute primitive roots modulo n is known

  • The number of primitive roots modulo n, if there are any, is equal to φ(φ(n))

    Example: 17 has 8 primitive roots modulo 17.
    φ(17) = 16 (Hint: 17 is a prime number)(Verify)
    φ(16) = 8 (Verify)

    Find all primitive root modulo 17

  • If the multiplicative order of a number m modulo n is equal to φ(n), then it is a primitive root. The converse is also true: If m is a primitive root modulo n, then the multiplicative order of m is φ(n)

Finding primitive root

  • First, compute φ(n). Then determine the different prime factors of φ(n), say p1, …, pk. Now, for every element m of Zn*, compute mφ(n)/pi mod n for i = 1, 2, 3…k
  • A number m for which these k results are all different from 1 is a primitive root

Discrete Logarithm Problem

Discrete logarithms are logarithms defined with regard to multiplicative cyclic groups. If G is a multiplicative cyclic group and g is a generator of G, then from the definition of cyclic groups, we know every element h in G can be written as gx for some x. The discrete logarithm to the base g of h in the group G is defined to be x.

Personally, I find it hard to deal with these generic a, b, c … terminology. Nothing better than an actual numeric example! So let’s take an example of Z5*

G = {1, 2, 3, 4}

If 2 is a generator, it has to generate all the elements modulo 5

20 ≡ 1 mod 5
21 ≡ 2 mod 5
22 ≡ 4 mod 5
23 ≡ 3 mod 5
24 ≡ 1 mod 5
25 ≡ 2 mod 5
…

Indeed, 2 is capable of generating all possible residues modulo 5 coprime to 5.

Following the definition above: All elements of G can be generated by the generator when raised to some power x

2x ≡ 4 mod 5

log2(element in G) = x

Discrete logarithm of 1 is 4 because 24 ≡ 1 mod 5
Discrete logarithm of 2 is 1 because 21 ≡ 2 mod 5
Discrete logarithm of 3 is 3 because 23 ≡ 3 mod 5
Discrete logarithm of 4 is 2 because 22 ≡ 4 mod 5

Discrete logarithm problem is defined as: given a group G, a generator g of the group and an element h of G, find the discrete logarithm to the base g of h in the group G.

In the above example, when the generator 2 is raised to a power x, the solution is equally likely to be any integer between 1 and 4. This creates our trap-door function. Strength of a one-way function is the time required to reverse it. Even with all the computational power on earth, it would take thousands of years to evaluate all possibilities.

Easy to perform in one way but hard to reverse.

Let’s look at a few more examples:

  • 2 is a primitive root of modulo 5
  • 3 is a primitive root of modulo 17
  • 3 is a primitive root of modulo 7

You may verify the repitition cycle here

Repetition and uniform distribution of solution

Distribution of powers of primitive root

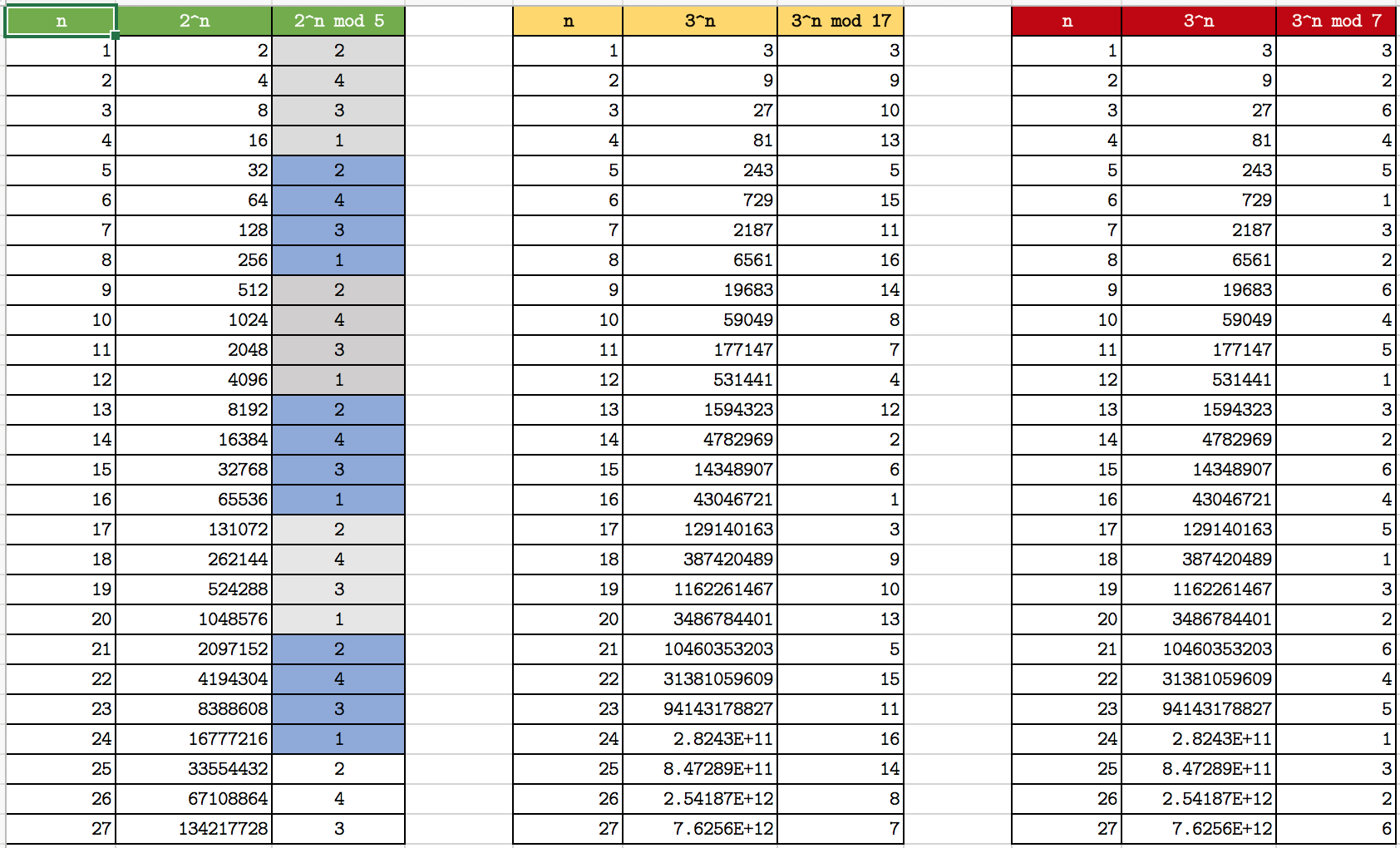
Considering our Z5* with (2 is generator): Calculating 3 by raising 2 with a power is trivial.
23 = 8 ≡ 3 mod 5

However, when you try to find out the powers that generate this element:

>>> for x in range(3, 100, 4):
...     print("2^" + str(x) + " mod 5 = " + str(2 ** x % 5))
...
2^3 mod 5 = 3
2^7 mod 5 = 3
2^11 mod 5 = 3
2^15 mod 5 = 3
2^19 mod 5 = 3
2^23 mod 5 = 3
2^27 mod 5 = 3
2^31 mod 5 = 3
2^35 mod 5 = 3
2^39 mod 5 = 3
2^43 mod 5 = 3
2^47 mod 5 = 3
2^51 mod 5 = 3
2^55 mod 5 = 3
2^59 mod 5 = 3
2^63 mod 5 = 3
2^67 mod 5 = 3
2^71 mod 5 = 3
2^75 mod 5 = 3
2^79 mod 5 = 3
2^83 mod 5 = 3
2^87 mod 5 = 3
2^91 mod 5 = 3
2^95 mod 5 = 3
2^99 mod 5 = 3

You observe that now the search space for this power is extremely large. Remember this was for a small prime number 5. Imagine the computational feasibility when the chosen prime is something like:

2519590847565789349402718324004839857142928212620403202777713783604366202070
7595556264018525880784406918290641249515082189298559149176184502808489120072
8449926873928072877767359714183472702618963750149718246911650776133798590957
0009733045974880842840179742910064245869181719511874612151517265463228221686
9987549182422433637259085141865462043576798423387184774447920739934236584823
8242811981638150106748104516603773060562016196762561338441436038339044149526
3443219011465754445417842402092461651572335077870774981712577246796292638635
6373289912154831438167899885040445364023527381951378636564391212010397122822
120720357

This prime number has 617 decimal digits (2048 bits). Now, I hope you can imagine the colossal computation required to find discrete logarithm of this number to the base of generator.

[Q] Is this discrete logarithm problem always hard?
[A] No. The hardness of finding discrete logarithms depends on the groups. For example, a popular choice of groups for discrete logarithm based crypto-systems is Zp* where p is a prime number. However, if p-1 is a product of small primes, then the Pohlig-Hellman algorithm can solve the discrete logarithm problem in this group very efficiently. That’s why we always want p to be a safe prime when using Zp* as the basis of discrete logarithm based crypto-systems. A safe prime is a prime number which equals 2q+1 where q is a large prime number. This guarantees that p-1 = 2q has a large prime factor so that the Pohlig-Hellman algorithm cannot solve the discrete logarithm problem easily.

  • Pohlig-Hellman algorithm
  • Baby step/giant step algorithm
  • Pollard’s ρ algorithm
  • Index calculus

If you’re wondering why there are no links to these methods, it’s because without reading those pages, I cannot vouch for their simplicity or help in enriching knowledge. Feel free to google up.

Attacks on DHKE

  1. Discrete logarithm computation: If Eve wants to determine gab given g, ga, gb, she could simply evaluate the discrete logarithm logg(ga) to compute a, and then evaluate (gb)a.

    Again, like with factorization, it is believed that general discrete logarithm computation is difficult with a standard (i.e., non-quantum) computer, provided the prime p is suciently large and not of any particularly special form (e.g., not such that p - 1 only has small prime divisors).

  2. Man-in-the-middle-attack: Imagine that an adversary Eve can intercept all communication between Alice and Bob. When Alice sends c1 = ga to Bob, Eve stores c1 and sends ge to Bob, for some random integer e known to Eve. Similarly, when Bob sends c2 = gb to Alice, Eve stores c2 and sends ge to Alice. Alice computes the key gae and Bob computes the key gbe. Eve can compute both keys. If Alice later sends an encrypted message to Bob using the key gae then Eve can decrypt it, read it, re-encrypt using the key gbe, and forward to Bob. Hence Alice and Bob might never learn that their security has been compromised. One way to overcome man-in-the-middle attacks is for Alice to send a digital signature on her value ga (and similarly for Bob). As long as Alice and Bob each hold authentic copies of the other’s public keys then this attack fails. There are various modications to the basic Die-Hellman algorithm that allow for mutual authentication: they are sufficiently distinct from the basic algorithm

  3. Imagine Alice and Bob are exchanging secure messages using a key generated by DHKE. Let’s say they both have a configured system with a private key and public parameters set to some values. Now, our evil Eve is quietly listening to these encrypted messages and recording all the packets. Eve continues to do this for almost a year. One fine morning, Eve gets access to Alice’s phone/computer and manages to extract the private key! (A real shame Alice isn’t careful with her stuff - I know). With this private key and other public information, Eve applies the right Math and ends up with the symmetric key Alice and Bob used so far. With this symmetric key, Eve decrypts all the session traffic captured so far. Guess what Eve stumbles upon! Bank account numbers, personal photos, personal messages, Alice’s VIN number, Alice’s DL number, and so on. (Don’t ask me why Alice had to share those numbers with Bob. People share all sorts of unwanted trash on social networks and this was a private chat, so why not?). So, it’s a big problem if every session doesn’t have a separate key.

DH in real life

Well, people outsmart people all the time. Classical textbook DH is no longer secure by itself. Even though the math (and DLP) stands strong, there are other ways of exploiting this key exchange protocol.

Various forms of DHKE:

  • Anonymous Diffie-Hellman: Diffie-Hellman, but without authentication. Since the keys used in the exchange are not authenticated, the protocol is susceptible to Man-in-the-Middle attacks. Anonymous Diffie-Hellman should not be used in any communication.

  • Fixed Diffie-Hellman embeds the server’s public parameter in the certificate, and the CA then signs the certificate. That is, the certificate contains the Diffie-Hellman public-key parameters, and those parameters never change. Diffie-Hellman parameters are signed with a DSS or RSA certificate.

  • Ephemeral Diffie-Hellman (DHE) uses temporary, public keys. Each instance or run of the protocol uses a different public key. The authenticity of the server’s temporary key can be verified by checking the signature on the key. Since the public keys are temporary, a compromise of the server’s long term signing key does not jeopardize the privacy of past sessions. This is known as Perfect Forward Secrecy (PFS). With DHE, a different key is used for each connection, and a leakage of private key would still mean that all of the communications were secure.

In TLS2, we often use DHE as part of a key-exchange that uses an additional authentication mechanism (e.g. RSA, PSK or ECDSA). So the fact that the SSL server signs the ephemeral public key implies to the SSL client that this Diffie-Hellman public key is from the SSL server. Within DHE-RSA, the server signs the Diffie-Hellman parameter (using a private key from an RSA key pair) to create a shared key.

  • ECDHE: Elliptic Curve Diffie Hellman Ephemeral
    Another way to achieve a Diffie-Hellman key exchange with the help of elliptic curve cryptography is based on the algebraic structure of elliptic curves over finite fields. Elliptic curve cryptography allows one to achieve the same level of security than RSA with smaller keys.

Elliptic Curve Cryptography needs an article for itself. I’ll post a link to it once I write it.

[Q] Why should one prefer ECDHE over DHE?
[A]

  • ECDHE is faster, for a given security level
  • The performance ratio increases with higher security levels (e.g. a 224-bit curve will give you roughly the same security as a 2048-bit plain DH key, leading to a factor of more than 8 in favour of the curve)
  • Smaller messages

Even Google chrome favors ECDHE over DHE

Additional Resources

Extras

In the fall of 1974, Ralph Merkle enrolled in CS244, the Computer Security course offered at UC Berkeley taught by Lance Hoffman. All students were required to submit two project proposals, one of which they would complete for the course. Ralph submitted a proposal for what would eventually become known as Public Key Cryptography – which Hoffman rejected!

After Hoffman rejected this proposal, he rewrote it to be shorter and simpler. Ralph resubmitted it to Hoffman. Hoffman continued to show little interest so he dropped the course, but kept working on the idea. Later, he showed an early draft to Bob Fabry, then on the faculty at Berkeley, who immediately recognized it as both novel and valuable and said “Publish it, win fame and fortune!”

Ralph submitted it to Susan Graham, then an Editor at the CACM in August of 1975. Graham sent his submitted paper out for review and received the following response from an “experienced cryptography expert” whose identity is unknown to this day:

“I am sorry to have to inform you that the paper is not in the main stream of present cryptography thinking and I would not recommend that it be published in the Communications of the ACM. Experience shows that it is extremely dangerous to transmit key information in the clear.”

With this blanket rejection of public key cryptography by an “expert”, CACM rejected the article. She was particularly bothered by the fact that “there are no references to the literature. Has anyone else ever investigated this approach. If they consider it and reject it, why?”

Ralph had failed to provide any references to the prior work on public key cryptography. The term “public key cryptography” did not yet exist, and there were no previous workers in the field.

As Ralph says: “This is not a unique problem: it illustrates a problem faced by anyone trying to explain a new idea to an “expert” who expects a properly referenced article anytime anyone tries to explain something to them.”

The first rejection by CACM left him confident that no one had previously investigated this approach, as the “experienced cryptography expert” had rather obviously failed to understand what was being proposed.

CACM eventually published the paper, though only after almost three years of delay

Credits

Footnotes

  1. In number theory, two integers a and b are said to be relatively prime, mutually prime, or coprime if the only positive integer (factor) that divides both of them is 1 (gcd(a, b) = 1) ↩

  2. Transport Layer Security is a cryptographic protocol designed to provide communications security over a computer network ↩